Kingdom Ken
- Newt

- May 5
- 6 min read
Updated: Sep 30
This is a game based on a problem in a 1970s textbook. It is a ken game (rock-paper-scissors game) of deceptive complexity. It has only 10 cards, but the rules of scoring make it far from simple to play.
Here is the full set of cards:

As with our other ken-based card games, players simultaneously flip over a card, but instead of a simple win-or-lose outcome, there are payoffs according to a table of scores. Plant wins are in pale green, Animal wins are in pale red. The payoffs are summed, and if the final answer is positive, the winner is the one who had the Animal cards, if negative, the winner is the player with the Plants.
This is the payoff table:
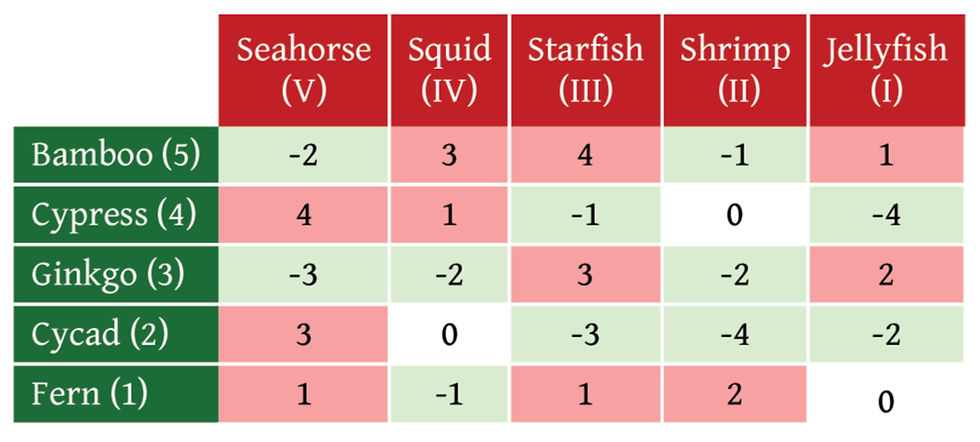
Another aspect that makes the game different to regular ken-games is that there are fewer kinds of cards available for each play as a round progresses, and the second last choice determines the final choice. So the strategy must change according to how the game has progressed. This means it's a game that lets you explore Nashian Game Theory and Bayesian reasoning. See below for more on the mathematics involved.
To play optimally, players must consider both overall success and immediate gain in each simultaneous card reveal, as they work against each other. The best first move may eliminate a lot of better moves from play. As play progresses through a round the strategies must change as the available card pool dwindles: there is always a different least worst play. This dynamic interplay between simultaneous and sequential decision-making transforms a simple card game into a complex exercise in strategic inference.
In the original example, Abner's game*, the cards are taken from a standard pack of cards. We wanted to correct the deliberate flaws in the original game, and also to make a dedicated pack. We chose icons to indicate creatures from the plant and animal kingdoms. For more information on what these broad kinds of plants and animals are, please read below.
There are five plant phyla, represented by Fern, Cycad, Ginkgo, Cypress, and Bamboo:

The plant cards all have green backs, numbered in Hindu-Arabic numbers reflecting their rising complexity.
Then there are five animal phyla, represented by Jellyfish, Shrimp, Starfish, Squid, and Seahorse:
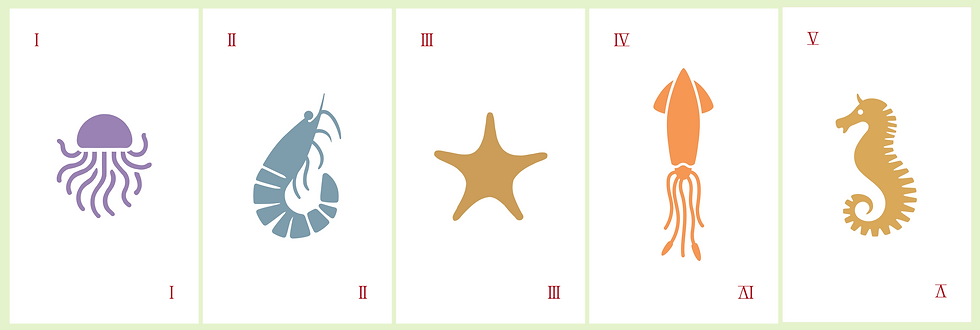
The animal cards all have red backs, numbered with Roman numerals.
There are three ways of playing Kingdoms, two are true Ken games, and one is more like a Whist game.
The Riggs mode, based on the original game, where cards are played as tricks, face down one at a time, then simultaneous flipping.
The Nash mode, where all the cards are laid out face down at the beginning of play, and flipped over one at a time.
The de Monfort mode, where one player leads and the opponent responds. This can alternate with trick winning or by turns.
There is more about these modes in the section below.
The two distributions (Plant and Animal wins) each have their own peculiarities, but by alternating the Kingdom assignment the players can ensure unbiased outcomes.
You can buy a pack printed on demand at Make Playing Cards online here,
Sample Games
Here is a sample game. Remember, the players play their cards simultaneously .
Alan (Animals) plays the Jellyfish, Pete (plants) plays the Fern, so the score is 0.
Alan plays the Shrimp, Pete plays Bamboo, with a payoff of -1. The score is now -1.
Alan then plays the Squid, Pete has played the Cycad, with a payoff of 0. The score remains at -1
There are now two cards left, so it is a choice of two possible outcomes. Alan plays the the Seahorse, Pete the Cypress. The payoff is +4, so the score is now 3
The remaining cards are the Starfish, and the Ginkgo with the payoff of 3, so the final score is 7. Alan wins.
The cards can also be used for Solitaire. The player chooses Plant or Animal to play, and after a shuffle the other cards are laid face down in a row. Here is a stop motion animation, made with the test cards during the design process.
The game ends up as a 0.
Jellyfish-Cypress -4
Shrimp-Bamboo -1
Starfish-Ginkgo 3
Squid-Fern -1
Seahorse-Cycad 3
By the way, if you want to try the game out, you can always make your own with business card blanks, or even 10 business cards you happen to have lying around. That is how we prototype most of our games. The play isn't as enjoyable, and they wear out, but if you're in a tight spot and want to play, it's fun.
Best games
This is one of the two the best outcomes for Plants, -1 + -3 + -2 + -4 + -2 = -12 :

This is one of the two best outcomes for animals 2+2+4+1+3:

Some oversimplified biology
In simple terms, Kingdoms (in the Linnaean system of classification) are top level distinctions as to kinds of living creatures. Creatures are classified according to their similarities, and these similarities at the most abstract are called Kingdoms. This game concentrates on two Kingdoms, the Plants (Plantae) and Animals (Animalae). N.B. Modern biology introduces a new level of classification above the Kingdom, the Domain, and Plants and Animals share the Eukaryote domain with Protists (kelp) and Fungi (Mushrooms and Toadstools).
Within those Kingdoms are Phyla (the plural of the Greek word Phylum), the next level down of the Linnaean classification system. We chose five classes from each of those kingdoms for our game, based on their ease of recognition.
Additionally as there were so few true plant species that live in water and so many animal species that do, we thought we would make a sea/land distinction. We've also designed them using contrasting approaches to the symbols and colours (by definition, plants are mostly green!).
Some oversimplified mathematics
The game has its origins in a textbook example designed to test the understanding of some aspects of Game Theory.
We know at the outset that there must be five tricks (four in the original example) from the matrix of 25. Each choice removes every payoff in that row and column, so something that looks like a good play may be disastrous if it locks out some good later outcomes,or worse, locks in some terrible ones.
There are only ten cards, yet there are still 5!², or 14,400 possible outcomes. How do we get that number? Even though there are only 10 cards(two sets of five, 5 + 5) and 25 squares in the payoff table (5 x 5), there are 14,400 possible games. To understand how that works imagine making a bracelet with five rounded beads, in five different colours. There are 120 ways to make that bracelet. This number is reached by multiplying by the number of choices left at each point, 5 x 4 x 3 x 2 x 1 = 120, something we call a factorial. Now imagine a second bracelet made with five diamond-shaped beads in five colours. That would also have 120 choices. But a bracelet that requires alternating round and diamond beads in five colours superimposes those choices making 120 x 120 = 14,400 choices altogether.
The three modes of playing all involve different amounts of knowledge
The Riggs mode, based on the original game, where cards are played as tricks, face down one at a time, then simultaneous flipping. This involves the challenges of Bayesian reasoning, as knowledge is discovered with each play. The possibilities left to play are ruled out by the previous ones.
The Nash mode, where all the cards are laid out face down at the beginning of play, and flipped over one at a time. The only knowledge at the beginning is the map of the card universe. This is much more like the traditional French Jeu de Societe, where risk is more important than reasoning.
Solitaire can be played with the cards in both these modes, the only difference is that you are playing against chance.
The third way of playing, is the whist mode, with a leader and a following player. This can alternate with trick winning or by turns. We call this the de Montmort mode, who analysed the probability involved in each turn of Whist in the 18th century treatise on the probability of card games.
Abner's Game
This is the example from the book.

The answer is that Abner has a slight advantage if played over a series of games.
The payoff table shows the asymmetries in the game. There are 6 successful outcomes for Spades, 8 for Hearts. But the distribution for Hearts makes payoffs harder.
In fact, it can be read from the score card that the best possible outcome for the player with the Spades is 9, while the best outcome for Hearts is 8. If you want to use conventional cards, the problem with Abner's Game can be corrected by the addition of the 10 of Hearts and the 10 of Spades, using the payoffs in the table above.













Comments